navigation banner skip navigation NIST Physical Measurement Laboratory home page go to NIST home page database home page Introduction and References Table of Atoms Table of Molecules

Introduction

Total cross sections for the ionization and excitation of atoms and molecules by electron impact is one of the essential sets of data needed in a wide range of applications, such as modeling plasmas for plasma processing of semiconductors, designing mercury-free fluorescent lamps, assessing the efficiency of ion gauges, normalizing mass spectrometer output, diagnosing plasmas in magnetic fusion devices, and modeling radiation effects on materials.

In addition to total ionization cross sections, sometimes differential ionization cross sections are needed. We present below total ionization cross sections for a large numbers of atoms/molecules, and singly differential ionization cross sections (energy distribution of ejected electrons) for H, He, and H2. Excitation cross sections for H, He, and Li are also presented.
 

A. Total Ionization Cross Sections

The accuracy of standard theoretical methods for ionization cross sections depends both on the quality of wave functions as well as the collision theory used. Many theories work well at high incident energies T but few can be trusted at low incident energies, particularly near the ionization threshold. Also, theories that require continuum wave functions are difficult to use on molecules because calculating continuum wave functions for molecules suitable for ionization cross sections is in general a very difficult task, particularly for polyatomic molecules. To date, major sources of ionization cross sections for molecules were experiments and theories--often semiempirical--that worked well only on limited types of targets and/or limited ranges of T.

The theory used in this ionization cross section database is specifically designed for electron-impact ionization. It is versatile and can provide cross sections for atoms as well as molecules. The theory, referred to as the Binary-Encounter-Bethe (BEB) model [1], combines the Mott cross section with the high-T behavior of the Bethe cross section. The theory does not use any fitting parameters, and provides a simple analytic formula for the ionization cross section per atomic/molecular orbital. The total ionization cross section for a target is obtained by summing these orbital cross sections. Four orbital constants--the binding energy B, the orbital kinetic energy U, the electron occupation number N, and a dipole constant Q--are needed for each orbital, and the first three constants are readily available from the ground-state wave function of the target atom or molecule. The basic formula for the ionization cross section per orbital is [1]:

equation (1) (1)

where t = T/B, u = U/B, S = 4πa02 N (R/B)2, a0 = 0.529 18 Å, and R = 13.6057 eV, and the dipole constant Q is defined in terms of the continuum dipole oscillator strength df/dW, where W is the kinetic energy of the ionized electron:

equation (2) (2)

When df/dW is unknown, one can put Q = 1 as a further approximation. The constant n on the right-hand side (RHS) of Eq. (1) is used for ion targets and valence orbitals of large atoms as indicated at the end of this section. Unless noted otherwise, use n = 1.

The BEB cross section is not very sensitive to the accuracy of the orbital constants used except for the value of the lowest B. A vertical ionization energy is recommended for the lowest B. We used an experimental value if it is known for a target. Otherwise theoretical values were used. The B values marked "OVGF" were calculated using the outer-valence Green's function method, those marked "CCSD" using the coupled cluster single double excitations, and those marked "CCSD(T)" using the CCSD plus triple excitations included perturbatively. Orbital constants obtained from the Hartree-Fock or similar wave functions are adequate. The resulting cross sections are accurate to 5 % to 20 % from threshold to T ~ 1 keV in most targets presented in this database.

As was demonstrated in a series of publications [1-11] the BEB model (with Q = 1 in most cases) was found to reproduce known ionization cross sections accurately for small atoms and a variety of large and small molecules from H2 to SF6. Also, the BEB model works well for radicals as well as stable molecules. In many cases, the theory agrees with experiments in peak values within 10 %. Unlike most theories, the BEB model is reliable near the threshold as well.

Production of a doubly charged ion or two singly-charged molecular fragments resulting from inner-shell ionization can be estimated by doubling the ionization cross sections of individual atomic/molecular orbitals whose binding energies B exceed the double ionization energy (approximately B > 40 eV) [6]. Inclusion of such contributions in the BEB theory is indicated by "Yes" in the atomic/molecular orbital constant column marked "DblIon," e.g., for C2F6 and C3F8 [7].

Through this WWW presentation, a user can (a) download orbital constants and ionization cross sections for an atom or molecule of interest as a text (ASCII file), (b) calculate the total ionization cross section at a given incident energy T online, (c) look at the graph for an atom or molecule with comparisons between the BEB model and experiments (data points for experiments, curves for theory unless otherwise specified), (d) zoom into a segment of the BEB cross section between specific incident energy limits, e.g., 5 eV to 100 eV, or (e) calculate the energy distribution of ejected electrons for H, He, and H2 online.

The molecules table and atoms table provide access to the data for those molecules and atoms to which the BEB model has been applied.

This database is updated frequently by adding new atoms and molecules as their cross sections become available. The BEB model is a simplified version of the BED model described in Section B below.

For singly-charged molecular ions, n = 2 is used on the RHS of Eq. (1) [Example: H2+]. Also, if the Mulliken population analysis of a valence molecular orbital indicates the leading component (> 50 %) consists of a specific atomic orbital with the principal quantum number n > 2, then this value of n is used in Eq. (1) [Example: CS2].

For atoms, if the principal quantum number (pqn) of an orbital is 3 or greater, then use n = pqn in Eq. (1). If pqn is 1 or 2, then use n = 1.
 

B. Singly Differential Ionization Cross Section (Ejected Electron Energy Distribution)

The singly differential cross section (SDCS) for ejecting an electron with kinetic energy W from an atomic/molecular orbital is given in the BED model by:

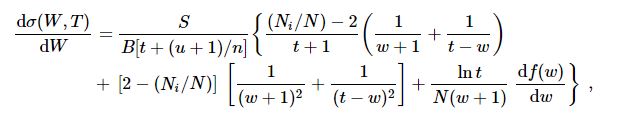equation (3) (3)

where w = W/B, df(w)/dw = the continuum dipole oscillator strength for ejecting an electron of kinetic energy W by photoionization, and Ni = the integral from 0 to infinity of(df/dw)dw. For H, He, and H2, known df/dw values have been fitted to a simple power series of y = B/(W + B),

equation (4) (4)

and the values of the coefficients a, b, ... and the corresponding SDCS are presented in the web pages of individual targets for T and W values requested by the user, or a table of SDCS for a T value and preselected values of W. The resulting dσ/dW is normalized to match the total ionization cross section. Sample comparisons between experimental data and theory for SDCS [9] are available online.

As is true for any theory, the BEB model for both total and differential cross sections has its limits. For instance, the BEB model presented here is a nonrelativistic theory, and therefore should not be used for T > 10 keV. For a relativistic extension of the BED/BEB model see [12].
 

C. Electron-Impact Excitation of Atoms

A scaling formula, called BE scaling, converts plane-wave Born cross sections (σPWB) for electron-impact excitation of neutral atoms to highly accurate cross sections at all incident energies T, although the original Born cross sections are reliable only at high T [13]. The BE scaled cross section σBE is defined as:

equation (5) (5)

where E is the excitation energy.

Scaling with just the excitation energy E, called E scaling, converts Coulomb Born cross sections (σ CB) for electron-impact excitation of singly charged atomic ions to highly accurate cross sections at all incident energies T, although the original Coulomb Born cross sections are reliable only at high T [14]. The E scaled cross section σE is defined as:

equation (6) (6)

D: Excitation-Autoionization

Total ionization cross sections of atoms and molecules consist of two components, direct and indirect ionization. The direct ionization accounts for the ejection of a bound electron directly into the continuum. The BEB/BED model is used to calculate direction ionization cross sections.

The most significant source for indirect ionization is the excitation of an inner-shell electron to an excited valence state (e.g., 3s → 3p excitation in aluminum), which is an unstable excited state. This excited state can decay by either emitting a photon or by ejecting an electron. The latter is called excitation-autoionization (EA). When the energy level of the excited state is not very high compared to the lowest ionization energy, EA dominates. For the ionization cross sections of atoms in this database, cross sections for significant EA (usually electric-dipole and spin allowed excitations) have been calculated using the BE and E scalings discussed in Section C above, and the EA cross sections are included in the total ionization cross sections.

BEB References

For further information, please contact:

Dr. Karl Irikura
Chemical and Biochemical Reference Data Division
National Institute of Standards and Technology
Gaithersburg, MD 20899-8320
phone 301-975-2510; fax 301-869-4020
email Feedback.

navigation banner NIST Physical Measurement Laboratory home page go to NIST home page Database home page Introduction and References Table of Atoms Table of Molecules