12.   Zeeman Effect

ΔE = gM µBB   .

(6)

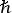The magnetic flux density is B, and µ_B is the Bohr magneton (µ_B = e/2m_e).  

The wavenumber shift Δσ corresponding to this energy shift is

Δσ = gM (0.466 86 B cm-1)  ,

(7)

with B representing the numerical value of the magnetic flux density in teslas. The quantity in parentheses, the Lorentz unit, is of the order of 1 or 2 cm^-1 for typical flux densities used to obtain Zeeman-effect data with classical spectroscopic methods. Accurate data can be obtained with much smaller fields, of course, by using higher-resolution techniques such as laser spectroscopy. Most of the g values now available for atomic energy levels were derived by application of the above formula (for each of the two combining levels) to measurements of optical Zeeman patterns. A single transverse-Zeeman-effect pattern (two polarizations, resolved components, and sufficiently complete) can yield the J value and the g value for each of the two levels involved.

Neglecting a number of higher-order effects, we can evaluate the g value of a level βJ belonging to a pure LS-coupling term using the formula
 

(8)

The independence of this expression from any other quantum numbers (represented by β) such as the configuration, etc., is important. The expression is derived from vector coupling formulas by assuming a g value of unity for a pure orbital angular momentum and writing the g value for a pure electron spin as g_e [15]. A value of 2 for g_e yields the Landé formula. If the anomalous magnetic moment of the electron is taken into account, the value of g_e is 2.002 319 3. "Schwinger" g values obtained with this more accurate value for g_e are given for levels of SL terms in Ref. 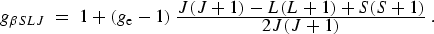[8].

The usefulness of g_SLJ values is enhanced by their relation to the g values in intermediate coupling. In the notation used in Eq. (4) for the wave function of a level βJ in intermediate coupling, the corresponding g value is given by
 

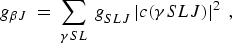
(9)

where the summation is over the same set of quantum numbers as for the wave function. The g_βJ value is thus a weighted average of the Landé g_SLJ values, the weighting factors being just the corresponding component percentages.

Formulas for magnetic splitting factors in the J₁ J₂ and J₁ L₂ coupling schemes are given in Refs. [8] and [15]. Some higher-order effects that must be included in more accurate Zeeman-effect calculations are treated by Bethe and Salpeter [4] and by Wybourne [15], for example. High precision calculations for helium are given in Ref. [16].