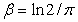Gaussian Filter
Gaussian filter is calculated by a direct convolution of the surface
topography with a Gaussian weighting function [1][2][3]. The weighting
function S(x,y)
is given by
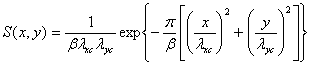
Where
x and y are the positions from the center of the weighting function
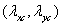 is the cutoff
wavelength at 50% attenuation ratio
is the cutoff
wavelength at 50% attenuation ratio
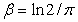
The transmission characteristic is 50% for the Gaussian Filter. So a single filter is customary to obtain both the roughness and waviness
surfaces.
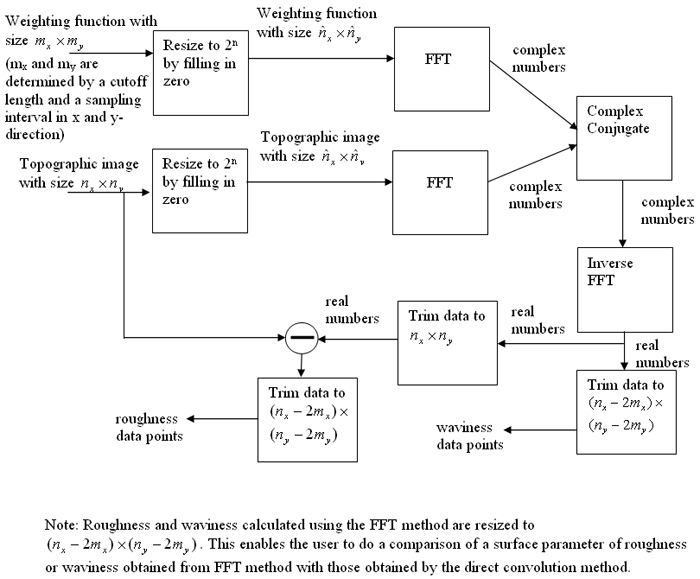
The convolution is the most common approach for Guassian filter. For increasing the speed,
the implementation by FFT was suggested by J. Raja and V. Radhakrishnan [4].
In the FFT approach, the spectrum of the original signal is computed by FFT algorithm. Then the
calculated spectrum is modified in frequency domain by a weighting function
according to the required filtering. The final filtered profile in time
domain is calculated by the inverse FFT of the modified spectrum.
The block diagram of this method for the Gaussian filter used in the system is illustrated in below.
References
1. Surface Texture (Surface Roughness, Waviness, and Lay), an American National Standard, ASME B46.1-2002, New York, NY
2. K. J. Stout, P. J. Sullivan, W. P. Dong, E. Mainsah, N. Lou, T. Mathia and H. Zahouani, The Development of Methods for The Characterisation of Roughness in Three Dimensions, Report EUR 15178 EN. EC Brussels, 1993
3. L. Blunt and X. Jiang, Advanced Techniques for Assessment Surface Topography, 1st edition, London Penton Press, 2003, ISBN 1903996112
4. J. Raja and V. Radhakrishnan, Filtering of Surface Profiles Using Fast
Fourier Transform, Int. of J. mach. Tool. Des. Res., Vol. 19, 133-141, 1979
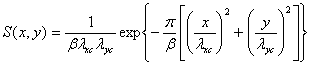
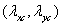 is the cutoff
wavelength at 50% attenuation ratio
is the cutoff
wavelength at 50% attenuation ratio