12. Other Current Concerns
Most of this description has been concerned with problems of
f′ or f1 and
f″ or
f2. Difficulties inherent in the form factor formalism as
opposed to the Modified Form Factor formalism or general S-matrix formalisms
are discussed elsewhere [46,47]. Use
of Modified Form Factors is of value at or above MeV energies for
various angles, where the separability of f0 and
f1 becomes questionable [10].
Sum rules have been discussed and investigated, particularly at relatively
low energies [48,49], and may be more
generally applied to theoretical or experimental data. Comparisons
of form factor predictions to others or to experiment without
allowance for the issues raised in this paper will endanger the
validity of conclusions drawn.
One of the major differences between these classes of theory, and in
particular between RDP, RMP [38,39] and
S-matrix methods [12] relate not to
f1 or f2 per se, but relate to the
relativistic correction factor frel. This contribution
indicates the correction for the high-frequency limit. For uranium at low
energies frel is of order -2.5 e/atom
[17-20], -1.5 e/atom [38,39], or
-1.2 e/atom [12,39]. The differences
between these theories are large, with a range at the 1 e/atom level
and an uncertainty quoted as ± 0.36 e/atom
[39]. Equally, for calcium
(Z = 20), quoted values vary from -0.06 eu to
-0.036 eu to -0.034 eu with, again, a quoted uncertainty of
± 0.009 eu [39]. These are
important and significant differences (particularly for medium and
heavy elements), although it should be clear that any comparison of
theories or experiments is difficult without correcting for the
effects discussed herein with their associated many-electron
errors. Issues regarding the forms for frel demand that input
values for f1 be calculated to better precision than the
uncertainty in the relativistic component. Errors of the preceding
sections or of integration or interpolation precision at this level
are unnecessary and obscure comparison of different models with
experiment.
The integration method adopted and discussed herein makes direct use
of the separation of orbitals and the assumption that the orbital
absorption coefficient is exactly zero below the edge. Correlation
between orbitals, excited bound states, level widths and resonance
phenomena may require alternate transforms based on
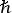ω = (0,∞) to (0,1) intervals. This
general issue was addressed by Cromer and Liberman
[17] and has been addressed more recently by
Wang and Pratt [50]. The presence of multiple
edges and near-singularities creates difficulty for most standard
integration methods. For comparison of theory to experiment, direct
measurement of Re(f) is required, but the current revised theoretical
calculation has an advantage over methods based on limited ranges of
experimental or synthesized attenuation coefficients, in avoiding
smoothing and other problems near edges.
A secondary difficulty, so far as published results are concerned,
relates to tabulations often being restricted to a small set of
Kα lines, or to other discrete sets
of energies which fail to reveal major variation of structure with energy.
