NIST: Diatomic Molecules - 2-Pi-Ground State Molecules

4. ²Π-Ground State Molecules

As in the case of the ³Σ-molecules, the energy levels of a ²Π-molecule exhibit the additional splittings due to the electron spin and orbital angular momentum interactions. In order to describe the rotational spectra of this class. Hund's coupling case (a) is employed as a starting point. The rotational levels are defined with the quantum number Ω, the absolute value of the projection of the total electronic angular momentum on the molecular axis, with the quantum number J which represents the total angular momentum from rotation and electronic motion, and with the parity. For NO the parity, + or -, of the levels split by Ω-doubling follows the notation of ref. [12]. Although the parity is not known for the other ²Π diatomic molecules, it is necessary to distinguish transitions of + ← - and - ← +. Here the notation a and b is used, where a refers to transitions between the higher energy Λ-doubled levels and b to the lower energy levels. If the molecule contains nuclei with non-zero spin, the coupling of J with I results in the total angular momentum quantum number, F, assuming coupling case (a_β). The spectral line table for NO uses the headings F₊ and F_ to indicate the Kronig symmetry and the total angular momentum quantum number.

The electric dipole transitions are given by the following selection rules: ΔΩ = 0, ΔJ = 0, ± 1, and + ↔ - plus the normal selection rule for hyperfine splittings, ΔF = 0, ± 1.

a. Molecular Parameters and Energy Level Formulation

The rotational energies, derived from the observed rotational transitions, can be described with the Hamiltonian [12]:

(eq20)

where a molecule-fixed cartesian coordinate system, with the z-axis along the molecular axis, is employed. The operators, L_z, L₊, and L_ are the three spherical components of the electronic orbital angular momentum; S_z, S₊, and S_ are the equivalent operators for electron spin and J_z, J₊, J_ for the total angular momentum. The parameters B, A, and γ are functions of the internuclear distance and, thus, may be defined in terms of a power series in $\zeta = \frac{r-r_{\rm e}}{r_{\rm e}}$ as:

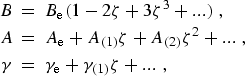eq20a (eq20a)

The eigenvalue solution of the Hamiltonian above is normally achieved by a perturbation method which takes into account the mixing of various vibrational states, and the mixing of various electronic states with the ground state. In this way centrifugal distortion terms, the vibrational dependence of the molecular parameters, l-uncoupling and Λ- or Ω-doubling can be determined.

There are a variety of possible approximations employed to describe the observed microwave spectra. The method used depends on how close the angular momenta coupling in a specific: molecule corresponds to Hund's coupling case (a). Formulations employed for intermediate coupling cases, like that for OH and NO, are given in ref. [13] and [14]. The determinable parameters are B_υ1 and B_υ2, the effective rotational constants for the ²Π_1/2 and ²Π_3/2, respectively, the centrifugal distortion parameters D_υ1 and D_υ2, and the Λ-doubling parameters α_p and β_p. A very detailed analysis of the Λ-doubling alone is given in ref. [12] while ref. [15] introduces an additional centrifugal term, δ, for the electronic distribution.

The appropriate formulation for coupling cases close to Hund's case (a), e.g., ClO and NS, are given in ref. [16]. The determinable parameters are B_υ1, B_υ2, D_υ1, D_υ2, where D_υ1 ≡ D_υ2, is assumed in all cases, and the Λ-doubling constant p_eff for the ²Π_1/2 state. Here p_eff is a function of α_p and β_p.

The rotational constant B_υ can be evaluated from B_υ1 and B_υ2, if additional assumptions are made. In a similar manner it is possible to estimate A and A₍₁₎ in a few instances.

The hyperfine coupling Hamiltonian given in ref. [10] is evaluated in ref. [14] to first order for the magnetic and nuclear electric quadrupole interactions. Although the first order perturbation treatment is adequate for the interpretation of the microwave spectra, the more detailed analysis in ref. [12] is necessary to adequately describe the radiofrequency spectrum of NO. The determinable parameters are the magnetic coupling constants a, b, c, and d, as well as the quadrupole coupling constant, eQq, which is proportional to the electric field gradient at the nucleus in the direction of the molecular axis, and $e Q \bar q$ , which is proportional to the field gradient perpendicular to the molecular axis. In molecules with coupling cases close to case (a), the determinable parameters are functions of combinations of the constants a, b, c, and d.

b. List of Symbols

B_υ1, B_υ2	Effective rotational constants in the ²Π_1/2 and ²Π_3/2 state, respectively, for the υ^th vibrational state (MHz).
D_υ1, D_υ2	Centrifugal distortion correction constants in the ²Π_1/2 and ²Π_3/2 state, respectively; D_eff, if D_υ1 = D_υ2 is assumed. (MHz).
α_p, β_p	Ω-doubling parameters,
		(eq21)
		(eq22)
p_eff	Λ-type doubling constant in the ²Π_1/2 state (MHz).
a, b, c, d	Magnetic hyperfine coupling constants (MHz) where,
	$a = 2\mu_{\rm B} g_{\rm N}\mu_{\rm N} \langle 1/r^3\rangle$	(eq23)
		(eq24)
		(eq25)
		(eq26)
	Here _μB is the Bohr magneton, _μN is the nuclear magneton, and g_N is the nuclear g-value.
eQq	Quadrupole coupling constant along the molecular axis, where $q = \left\langle {\displaystyle \frac{3\cos^2\chi-1}{r^3}}\right\rangle$ (MHz).
$e Q \bar q$	Quadrupole coupling constant perpendicular to the molecular axis, where $\bar q = \left\langle {\displaystyle \frac{3\sin^2\chi}{r^3}}\right\rangle$ (MHz).
A	Spin-orbit coupling constant defined by the power series, expansion, $A&=&A_{\rm e} + A_{(1)} \zeta + A_{(2)} \zeta^2 + ... ~ .$
_γ	Spin-rotation coupling constant defined by the power series $\gamma&=&\gamma_{\rm e} + \gamma_{(1)} \zeta + ... ~ .$

4. 2Π-Ground State Molecules

a. Molecular Parameters and Energy Level Formulation

b. List of Symbols

4. ²Π-Ground State Molecules