

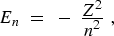 |
(10) |
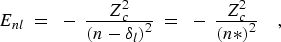 |
(11) |
If the core has one or more open subshells, the series limit may be the baricenter of the entire core configuration, or any appropriate sub-structure of the core, down to and including a single level. The Enl values refer to the series of corresponding (core)nl structures built on the particular limit structure. The value of the quantum defect depends to some extent on which (core)nl structures are represented by the series formula.
The quantum defect in general also has an energy dependence that must be taken
into account if lower members of a series are to be accurately represented by
Eq. (11). For an unperturbed series, this dependence
can be expressed by the extended Ritz formula
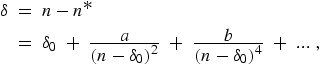 |
(12) |
with δ0,a,b... constants for the series (δ0 being the limit value of the quantum defect for high series members) [17]. The value of a is usually positive for core-penetration series and negative for core-polarization series. A discussion of the foundations of the Ritz expansion and application to high precision calculations in helium is given in Ref. [18].
A spectral-line series results from either emission or absorption transitions involving a common lower level and a series of successive (core)nl upper levels differing only in their n values. The principal series of Na I, 3s 2S1/2 - np 2P�1/2,3/2 (n ≥ 3) is an example. The regularity of successive upper term values with increasing n [Eqs. (11), (12)] is of course observed in line series; the intervals between successive lines decrease in a regular manner towards higher wavenumbers, and the series of increasing wavenumbers converges towards the term value of the lower level as a limit.