

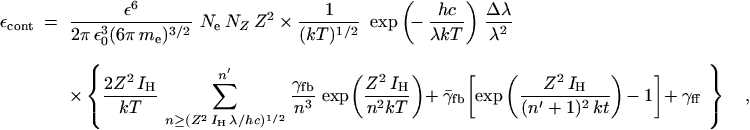 |
(44) |
where Ne is the electron density, NZ the
number density of hydrogenic (bare) ions of nuclear charge Z,
IH the ionization energy of hydrogen, n′ the
principal quantum number of the lowest level for which adjacent levels are so
close that they approach a continuum and summation over n may be
replaced by an integral. (The choice of n′ is rather arbitrary;
n′ as low as 6 is found in the literature.)
γf b and γf f are the Gaunt
factors, which are generally close to unity. (For the higher free-bound
continua, starting with n′ + 1, an average Gaunt factor
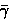 f b
is used.) For neutral hydrogen, the recombination continuum forming
H- becomes important, too [35].
f b
is used.) For neutral hydrogen, the recombination continuum forming
H- becomes important, too [35].
In the equation above, the value of the constant factor is 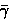 f b,
γf f have been assumed to be unity.]
f b,
γf f have been assumed to be unity.]
Near the ionization limit, the f values for bound-bound transitions of a spectral series (n′ → ∞) make a smooth connection to the differential oscillator strength distribution df/dε in the continuum [38].