

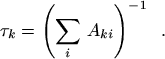 |
(27) |
The branching ratio of a particular transition, say to state
i ′, is defined as
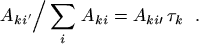 |
(28) |
If only one branch (i ′) exists (or if all other branches
may be neglected), one obtains
Aki ′ τk = 1, and
| (29) |
Precision lifetime measurement techniques are discussed in Atomic, Molecular, & Optical Physics Handbook, Chaps. 17 and 18, ed. by G.W.F. Drake (AIP, Woodbury, NY, 1996).
|
|
(30) |
Hydrogenic Z scaling. The spectroscopic quantities for a
hydrogenic ion of nuclear charge Z are related to the equivalent
quantities in hydrogen (Z = 1) as follows (neglecting small
differences in the values of RM):
| (31) | |
| |
(32) |
| |
(33) |
| |
(34) |
| |
(35) |
For large values of Z, roughly Z > 20, relativistic corrections become noticeable and must be taken into account.
f-value trends. f values for high series members (large
n′ values) of hydrogenic ions decrease according to
| (36) |
Data for some lines of the main spectral series of hydrogen are given in the table below.
| Transition | Customary name a |
λ
b (Å) |
gi c | gk | Aki (108 s-1) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1-2 | (Lα ) | 1 215. | 67 | 2 | 8 | 4.699 | ||||
| 1-3 | (Lβ ) | 1 025. | 73 | 2 | 18 | 5.575(-1) d | ||||
| 1-4 | (Lγ ) | 972. | 537 | 2 | 32 | 1.278(-1) | ||||
| 1-5 | (Lδ ) | 949. | 743 | 2 | 50 | 4.125(-2) | ||||
| 1-6 | (Lε ) | 937. | 80 | 2 | 72 | 1.644(-2) | ||||
| 2-3 | (Hα ) | 6 562. | 80 | 8 | 18 | 4.410(-1) | ||||
| 2-4 | (Hβ ) | 4 861. | 32 | 8 | 32 | 8.419(-2) | ||||
| 2-5 | (Hγ ) | 4 340. | 46 | 8 | 50 | 2.530(-2) | ||||
| 2-6 | (Hδ ) | 4 101. | 73 | 8 | 72 | 9.732(-3) | ||||
| 2-7 | (Hε ) | 3 970. | 07 | 8 | 98 | 4.389(-3) | ||||
| 3-4 | (Pα ) | 18 751. | 0 | 18 | 32 | 8.986(-2) | ||||
| 3-5 | (Pβ ) | 12 818. | 1 | 18 | 50 | 2.201(-2) | ||||
| 3-6 | (Pγ ) | 10 938. | 1 | 18 | 72 | 7.783(-3) | ||||
| 3-7 | (Pδ ) | 10 049. | 4 | 18 | 98 | 3.358(-3) | ||||
| 3-8 | (Pε ) | 9 545. | 97 | 18 | 128 | 1.651(-3) | ||||
| Z-2 E = E0 + E1 Z-1 + E2 Z-2 + ... , | (37) |
| Z2 S = S0 + S1 Z-1 + S2 Z-2 + ... , | (38) |
| f = f0 + f1 Z-1 + f2 Z-2 + ... , | (39) |
For equivalent transitions of homologous atoms, f values vary
gradually. Transitions to be compared in the case of the "alkalis"
are [34]
![\begin{eqnarray*}
(nl-n^\prime l^\prime)_{\rm Li}&\rightarrow& \left[ (n+1)l-(n^\prime+1)
l^\prime \right]_{\rm Na}\\
&\rightarrow& \left[ (n+2)l-(n^\prime+2) l^\prime \right]_{\rm Cu}~\rightarrow~\ldots \quad .
\end{eqnarray*}](Eqs/alkalis.gif) |
(Eq) |
Complex atomic structures, as well as cases involving strong cancellation in the integrand of the transition integral, generally do not adhere to this regular behavior.