 |
 |
 |
In isolation, these tables provide form factors, attenuation and scattering cross-sections for Z = 30-36 from E = 0.9 keV to E = 6.58 keV; for Z = 60-74, from E = 0.1 keV to E = 3.98 keV; and for Z = 75-89, from E = 0.5 keV to E = 8.54 keV. These regions relate directly to the regions of interest in the text, and are the regions where significant improvement has been made. Additionally we provide in Table 6 a coarse grid for Z = 30-36, Z = 60-89 from 0.1 keV to 10 keV following the "Grodstein grid" energies used in earlier tabulations and by other researchers.
Values for f1, f2 or [µ/ρ]PE should be extracted from the tables for the given element(s) and energies required. Linear interpolation of f1 should be adequate, while linear log-log interpolation of f2 or [µ/ρ]PE should be adequate on this scale, if required.
The energy range covered exceeds that for normal x-ray diffraction and crystallography studies but allows limitations and specialized experiments to be investigated with reference to updated and corrected theory. Discussion of solid target effects, correlation, nuclear resonances and uncertainties should be noted carefully in applications below 1 keV or above 100 keV.
The tabulation provides a sufficiently fine grid with accurate atomic edge structure to allow such experiments as DAFS (diffraction anomalous fine structure) to investigate fine structure and spatial distribution of atoms and electrons within materials [58]. Multilayer diffraction experiments may be pursued at lower energies in an analogous manner.
Table 6 presents results for the Grodstein grid energies in this region from 0.1 keV to 10 keV, particularly for comparison to other or earlier tables without interpolation. Although the interpolation process is very straightforward, it has been found that this brief summary is often useful for non-synchrotron applications.
For comparisons to other results in the forward scattering limit where the
momentum transfer q = 0, the value of
f0 = Z may be used and the real and
imaginary components of f are then fully defined. As an example, the
forward scattering limit for copper at 10.32 keV, in electrons per atom,
is
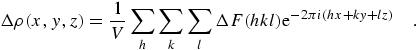 |
(eq 11) |
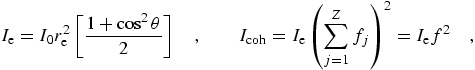 |
(eq 12) |
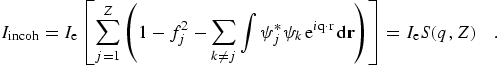 |
(eq 13) |
In these equations, fj is the form factor for an individual orbital, leading to the sum f for the atomic form factor. Corresponding integrated cross-sections, as presented in sum in C95, this work, and (for example) refs. [2] and [13] are given by
| (eq 14) |
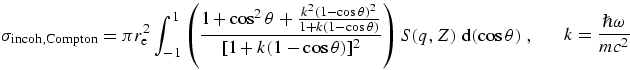 |
(eq 15) |
where the large bracketed factor represents the recoil process for a free electron as given by the Klein-Nishina formula [74] and the binding effects are included by the incoherent scattering function I(q,Z) or S(q,Z).
However, for N atoms in a unit cell of volume Vc, the
coherent scattering in a Bragg reflection should be summed in phase to give
This is a much larger value than the Rayleigh computation, and assumes
alignment of the Bragg planes near a Bragg condition. The corresponding thermal
diffuse scattering approximation assumes the scattering crystal is explicitly
misaligned from any Bragg conditions, and leads to a much lower cross-section
Corresponding formulae may be found in refs. [2],
[13], [19] and
[68] for differential cross-sections. Because these
various formulae have significant energy and angular dependence, and vary
dramatically from monatomic gas to aligned or misaligned solid, it is often
advisable to compute the scattering cross-sections directly rather than to use
a simple approximation. However, the full version of the incoherent
cross-section cannot be computed from the data in C95 or this work, because we
do not present the orbital wavefunctions needed to compute the interference
term of S(q,Z). It is however possible to compute the
coherent cross-sections in any approximation, and to compute the estimates of
S(q,Z) omitting that last term. For most low or
medium-energy purposes this is quite adequate, but we also present the sum of
coherent and incoherent cross-sections under the assumption of Rayleigh
scattering, in the tabulation.
is observed. These latter two coefficients are angle-dependent and may in part
be determined from appropriate structure factors for a given crystal
orientation as described above. However a column is provided for the sum of
these two latter coefficients in an average-over-angles for an atomic scatterer
[45], [75]. These
references should be consulted for details concerning the approximation
involved, although the column in the current tabulation is a new computation of
the sum (following C95). The main assumption is that Bragg-Laue peaks and
troughs are avoided, or that the material is randomly oriented and preferably
mosaic. If this is not true, it may be necessary to compute the dynamically
diffracted intensities from the structure factor rather than rely on the
approximation. However, simply summing these two columns allows the comparison
of theory to experimental attenuation data. For most regions of interest for
medical imaging, this is an adequate approximation. The accuracy of the
scattering coefficients (within the Rayleigh approximation) is of order
5 %.
At 1 MeV energies and above, (or at γ-ray resonances), nuclear physics dominates and we recommend
inclusion of corrections by Hubbell et al. [12,13]
for radiative and double-Compton contributions to incoherent cross-sections,
reaching 1 % at 100 MeV energies, and those of nuclear-field pair
production κn beginning at
The isolated K-shell cross-section is also important for experimental
diagnostics and corrections. In particular, fluorescence yields from atoms are
negligible for almost all orbitals except the K-shell, when compared to Auger
and Coster-Kronig transitions. However, the fluorescence yield fraction for the
K-shell is large, so the dependence of the cross-section upon energy is equally
important. The qualitative result in an experimental ion chamber is significant
- the fluorescence x-ray may escape from the ion chamber without conversion to
(detectable) ion pairs. A more detailed discussion of this is provided
elsewhere [42].
Poisson's equation relates the potential and charge distributions, and leads to
the Mott-Bethe formula for fB(q,Z) in terms of
the x-ray atomic form factor f(q,Z):
On the basis of these formulae, numerous studies can be and have been conducted,
and we refer simply to two summaries for elastic and inelastic scattering
[77,78].
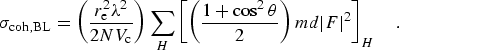
(eq 16)
or
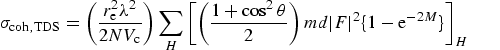
(eq 17)
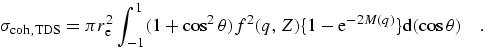
(eq 18)
8.8 X-Ray Attenuation [Medical imaging, transmission studies]
For filters or filter materials, the photoelectric attenuation coefficient is
provided in order to compare to appropriate experiments or to allow for objects
in a beam-line. The conversion to this from f2 in appropriate
units is provided at the top of the table. Use of barns/atom is also common,
and the conversion factor for this is also provided. Often this column is not
measured, and only the total observed mass attenuation coefficient
![]()
(eq 19)
8.9 [High-energy] Radiation Shielding
For high energies (the transition depends upon Z), the coherent and
incoherent cross-sections dominate over the photoelectric cross-section. In t
his region the scattering coefficients of refs. [2] and [13] are recommended as
a possibly higher precision computation. At this point the experimental
evidence on this point is inconclusive, but we do not claim any higher accuracy
than 5 % for these scattering estimates. At high energies there may also
be interference between the photoeffect and coherent cross-sections, in which
case the current tabulation is important in identifying such effects but not in
computing them.
8.10 VUV reflectivities and multi-layer computations
In addition to the discussions in refs. [6-8],
relating to multilayer theory, experimental investigations in the VUV region
suffer from the limited precision of theory (and of this current work). Our
best recommendation regarding the estimation of either the magnitude of the
form factor for an element in this region, or for a structural feature in this
region, is to compare the results of the current approach to that of
ref. [33], and to treat the difference as an
estimate of the theoretical uncertainty in the region. The major problems arise
from valence shell correlations, and hence poor convergence of orbitals, and
from correlated excitations, phonons and other solid state interactions. At the
current time, we only present the results of C95 and this work as a guide in
the region below 100 eV.
8.11 Individual orbital cross-section studies, and fluorescence yields
The column providing the photoabsorption coefficient for the K-shell only is
included for two purposes. The first is that at high energies this is the
dominant contribution to the total photoabsorption, and provides a guide for
the local energy dependence of the cross-section. Secondly, it serves as an
illustration of the isolation of individual orbital cross-sections,
particularly for higher energies.
8.12 Comparisons to literature
The plots provide comparison to the theoretical results of Scofield
[28,29], [34] the
experimental compilation of Saloman et al. [34], and
the experimental synthesis of Henke et al. [32,33].
This is considered by the author to be the most useful and convenient
comparison of current work in the literature. Scofield is often cited and the
original stimulation for the preparation of this work was a comparison with
that theory. The plots indicate limitations regarding restricted ranges and
tabulation steps, show good agreement over much of the energy range for many
elements, and indicate regions of divergence, difficulty or concern. Some of
these concerns have been addressed directly in this paper, while others remain.
A naïve statement of uncertainty in Henke or this work arises from the
divergence between the two. This may relate to local structure, absolute
values, or global structure. An alternate error estimate is provided in
Table 2.
8.13 Chemical Shifts
The edge energies used follow ref. [76] are
provided at the top of each table so that criticism (or experimental
investigation) may indicate a shift of the local energy scale which may
be appropriate in a specific material or experiment. This is not encouraged or
recommended; nonetheless, it is provided as a statement of the assumptions and
basis of the computation.
8.14 Electron form factors and scattering
Within the isolated atom approximation for spherically symmetric atoms, the
electron atomic form factor is given by an analogue of
(eq 5), with the electron density replaced
by the periodic potential φ(r):
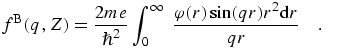
(eq 20)
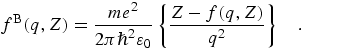
(eq 21)
8.15 X-Ray Anomalous Fine Structure (XAFS) and Diffraction Anomalous Fine
Structure (XAFS)
X-Ray Anomalous Fine Structure (XAFS) studies typically use a scaled reference
line for atomic structure, relative to which the bonding, nearest neighbor,
and structural information is extracted. This reference line should be derived
from atomic theory for an isolated atom. If this reference theory were accurate
to better than 1 %, XAFS and DAFS would be consistent and provide
unambiguous determination of local structure. Not all theories provide a
self-consistent reference for atomic theory near edges, which is a
pre-condition for the correct interpretation of fine structure measurements.
![]()
![]()
![]()
![]()