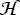Diatomic Spectral Database

3. 3Σ-Ground State Molecules

The O2 and SO molecules are the only diatomic molecules in this compilation which possess a 3Σ electronic ground state. Since the energy level calculations differ quite markedly from those in section 2, a detailed description of the calculations will be given here. Although a number of authors have treated this problem in slightly different manners than that discussed below, for uniformity we have chosen the formulation which corresponds closest to that employed in the previous section.

In order to describe the rotational spectra of this class, Hund's coupling case (b) was chosen as the starting point. The rotational levels are characterized by the rotational angular momentum quantum number, N, and the resultant angular momentum quantum number, J, which includes the total electron spin angular momentum. If the molecule has nuclei with non-zero nuclear spin, I, these are coupled to J to form the total angular momentum quantum number F, whereby coupling case (bβJ) is assumed here. For pure case (bβJ) the electric dipole transitions occur with the selection rules: ΔN = � 1, ΔF = 0, � 1, and ΔJ = 0, � 1, in the absence of external fields. Since an intermediate coupling case is actually observed, transitions are allowed for ΔN = � 3. The magnetic dipole transitions occur with the selection rules: ΔN = 0, � 2 and ΔJ = 0, � 1.  

a. Molecular Parameters and Energy Level Formulation

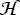The rotational energy levels may be described with the Hamiltonian [8]: Hamiltonian = 2/3 λ(3Sz2 - S2) + γ(N · S) + BN2 whereby a molecule fixed cartesian coordinate system is employed with the z-axis along the molecular axis. The first term describes the spin-spin interaction, the second term refers to the spin-rotation interaction and the last term describes the rotational kinetic energy. Since the coefficients λ, γ and B are functions of the internuclear distance, r, centrifugal distortion and vibration-rotation interactions arise. If we define the coefficients as follows:

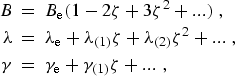eq10 (eq10)

where $\zeta = \frac{r-r_{\rm e}}{r_{\rm e}}$, the vibrational state dependence of the molecular parameters is given by:

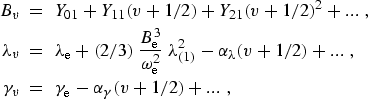eq11 (eq11)

where the Dunham coefficients, Ylj , are defined in section 2 and

eq12 (eq12)

eq13 (eq13)

The centrifugal distortion terms are defined as:

eq14 (eq14)

eq15 (eq15)
and
eq16 (eq16)

With these definitions, the rotational energy levels are given in the form [9]:

eq17 (eq17)

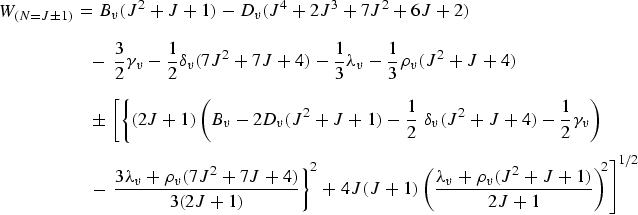eq18 (eq18)

The sextic terms, Hυ, of the rotational energy are neglected because they cannot be determined from the data presently available for the spectral observations on 3Σ electronic ground state molecules. The energy equations are utilized with the selection rules stated above to allow the determination of the molecular constants  Bυ, λυ, γυ, Dυ, ρυ, and δυ, for vibrational state υ. Combining the data available for various vibrational states allows the derivation of potential coefficients, ai, and the expansion parameters of λ and γ.

Magnetic hyperfine structure has been described by Frosch and Foley [10] in terms of the determinable parameters, b and c. The nuclear electric quadrupole hyperfine structure is described by Amano, et al. [11] and results in determination of the constant, eQqυ, as defined in the discussion of 1Σ ground electronic state molecules.

b. List of Symbols

Symbols (See section 2b for additional definitions.)
ai Dunham potential coefficients.
λυ  Spin-spin coupling parameter in the υth vibrational state (MHz).
αλ  Spin-spin vibrational constant (MHz).
γυ  Spin-rotation coupling parameter in the υth vibrational state (MHz).
αγ  Coefficient in the power series expansion of γυ.
ρυ Centrifugal distortion correction to λυ (MHz).
δυ Centrifugal distortion correction to γυ (MHz) .
λe, λ(1), λ(2) Expansion coefficients of λ in a power series of ξ.
γe, γ(1) Expansion coefficients of γ in a power series of ξ.
b, c Magnetic hyperfine coupling constants:

eq19a (eq19a)
eq19b (eq19b)
where µB is the Bohr magneton, µN the nuclear magneton and gN, the nuclear g-valve.

Back to the Diatomic Spectral Database Main Page
previous    next