 |
 |
 |
In the intermediate energy range, typically from 0.01-0.1 keV through to 80-800 keV, the interaction of the incident photon with the electrons, i.e., with the bound atomic orbitals, without production of secondary x-rays of reduced energy, is the dominant process. The photon is then either scattered without altering the internal energy of the atom, or it is absorbed. This absorption is usually into a single atomic orbital, with a consequent ejection of a photoelectron and production of a singly-ionized species.
Both photoabsorption and (Rayleigh) scattering are described by the structure factor F of the material in condensed or gas phase. In particular, diffracted intensity or coherent scattering is a complicated function of F, but for weak reflections is linear or quadratic in F. Equally, transmission through a bulk material is a complex function of F but local attenuation is a relatively simple function of the imaginary component of F [3-5]. This is well known in the crystallographic community and is used extensively in the multilayer community at lower energies [6-8]. The structure factor for a given reflection (denoted hkl from the Miller indices) is a sum over the atoms in the appropriate lattice (for a crystal) of the atomic form factors or the x-ray scattering factors fj of the jth atom:
| (eq 1) |
At grazing angles of incidence with solids, photons interact with the surface, and the photoabsorption and reflection processes may be given by Fresnel equations (while still dominated by electron orbital interaction and governed by the structure factor and form factors) [9]. If the atoms in a condensed system may be considered to scatter as dipoles (i.e., for low energies or small scattering angles) then the interaction of x-rays with matter may be described using optical constants such as the complex index of refraction nr or the complex dielectric constant ε(E), which are related to the form factors by
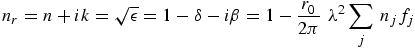 |
(eq 2) |