2. Form Factors and Standard Definitions
The real part of the atomic x-ray scattering factor is
[10]
where f′(E,Z)
=f+ + frel is composed of the
non-relativistic anomalous dispersion f+ and the
relativistic correction factor frel.
f0(q,Z) is the `normal' coherent scattering
factor as a function of momentum transfer
q = |Kf - Ki|
= (4πsin
θ/λ),
the latter relation for elastic scattering through an angle
2θ.
The dependences of f upon q and E may not be
strictly separable as implied by the separation into f0
and f′. Because of this,
some authors define a modified form factor MFF (g)
[11] or anomalous scattering factors
(g′ and
g″)
[12]. The nuclear Thomson
scattering (NT) is small and negative in phase
relative to the electronic form factor
(f0+f′),
of magnitude
fNT = -Z2m/M,
with small (negligible) energy and momentum dependence
[13,14]. The S-matrix channels of nuclear
photo-effect (dipole resonance), pair-N, pair-e production and
Delbrück scattering and other, smaller effects are typically
neglected, providing upper limits in energy for the validity of these
syntheses.
The imaginary part of the dispersion correction is simply linked to the
photoeffect cross section
µPE(E)
(neglecting, or including, bound-bound cross-sections) at the
photon energy E:
f1 and f2 are used in Refs.
[7,15,16]. The form factor f1
is particularly useful in illustrating effects described herein because
it approximates Re(f) in the forward scattering direction where
f0 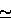 Z
and hence estimates the total scattering factor, placing the problems
indicated on an absolute footing. It is also appropriate in typical
experiments. The standard dispersion relation yields
Z
and hence estimates the total scattering factor, placing the problems
indicated on an absolute footing. It is also appropriate in typical
experiments. The standard dispersion relation yields
Here E = 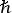 ω is the x-ray energy,
ε′
is the energy above the electron binding energy of the intermediate (bound
or continuum) state, and P represents the principal value. Commonly the
equation may be separated by orbital or by electron, with neglect of
unoccupied bound states yielding
ω is the x-ray energy,
ε′
is the energy above the electron binding energy of the intermediate (bound
or continuum) state, and P represents the principal value. Commonly the
equation may be separated by orbital or by electron, with neglect of
unoccupied bound states yielding
where -ε1 is
the electron binding energy, and
ε+
is the (continuum) energy. The high-energy constant may be combined with
relativistic correction factors to provide the separation into
frel and f+ as indicated above.



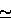 Z
and hence estimates the total scattering factor, placing the problems
indicated on an absolute footing. It is also appropriate in typical
experiments. The standard dispersion relation yields
Z
and hence estimates the total scattering factor, placing the problems
indicated on an absolute footing. It is also appropriate in typical
experiments. The standard dispersion relation yields
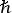 ω is the x-ray energy,
ε′
is the energy above the electron binding energy of the intermediate (bound
or continuum) state, and P represents the principal value. Commonly the
equation may be separated by orbital or by electron, with neglect of
unoccupied bound states yielding
ω is the x-ray energy,
ε′
is the energy above the electron binding energy of the intermediate (bound
or continuum) state, and P represents the principal value. Commonly the
equation may be separated by orbital or by electron, with neglect of
unoccupied bound states yielding