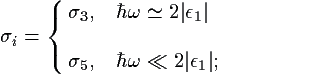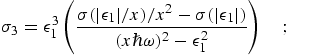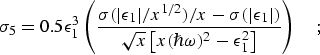4. Basic Transform Equations
Appropriate formulae based on (eq 7)
should give a small and smooth integral over the
range of the integrating variable, with the dominant term given
by analytic form.
The situation may be illustrated by considering the above-edge case, given
by Eq. 27 of Ref. [17]:
with α the fine structure
constant and energies and σ
in atomic units (au). Gauss-Legendre integration points are fixed by the
order of the integration, but corresponding energies may be adjusted to
optimize the precision for a particular photon energy by
scaling (contracting or expanding) the integrating variable, following
(but in contrast to) Eq. 29 of Ref. [17]
[for Eq. (8)]:
Note that
ε+>0 and
-ε1>0 and
the integration limits are transformed from
(0,∞) to (1,0), while in the first case
σ(ε+ -
ε1) becomes
σ(-
ε1/x).
By symmetry, this yields a well-defined integral which properly
ranges from 0 to 1.
Following the same formalism as in [17-20],
improved if not fully optimized relations for f+ may then be
given as
for 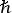 ω > |ε1| (above the edge).
At the edge, use
ω > |ε1| (above the edge).
At the edge, use
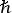 (ω + δω) to avoid the
computational singularity. Below the edge
(|ε1| >
(ω + δω) to avoid the
computational singularity. Below the edge
(|ε1| > 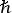 ω),
ω),
where, again, σ(|ε1|)
is given by
σ(|ε1|(1+δ)) to arbitrary precision.
The second terms of (eq 10) and
(eq 15) are always negative, while the first term in
(eq 10) is positive and the first
term in (eq 15) is negative. Use of (these)
appropriate functions
can lead to problems where integration points would lie well beyond the
database (11 data points per orbital). In such cases, the above-edge or
below-edge behaviour should be retained, but the choice of form may be
modified appropriately to match the data and to optimize precision.
The effects of this formalism and these specific modifications,
compared to the earlier results, may be seen generally near edges,
at energies below 2 keV or above 70 keV, but also at intermediate
energies.



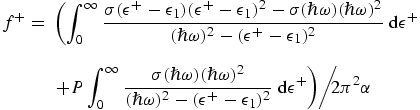
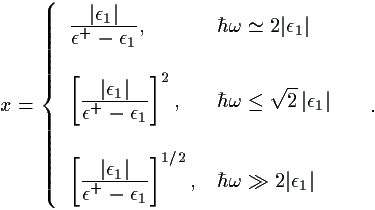
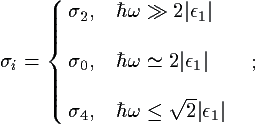
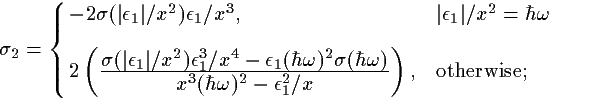
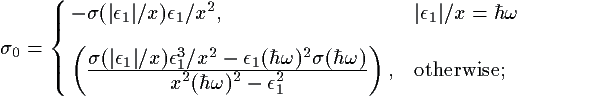
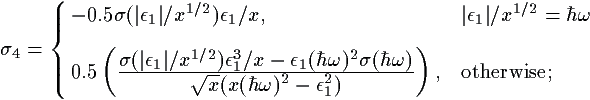
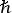 ω > |ε1|
ω > |ε1|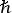 (ω + δω)
(ω + δω)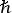 ω),
ω),