5. Avoidance of Singularities in
f′(E) Above Edges
The functional forms of the integral of
f″ as indicated in
Refs. [17-20] are formally continuous above each
edge but include singularities in both numerator and denominator (which cancel).
Consequently, the code of Cromer and Liberman [17-20]
yields divide-by-zero errors for Z = 18 (argon, 1.28 keV)
and elsewhere at energies for Z > 2 corresponding to
cancellations (5 per orbital).
The functional forms indicated [17-20] were
otherwise appropriate and valid in the 5 keV-50 keV range. This
was the main concern of the authors, but extension beyond this range in
either direction requires reevaluation of the construction. In
particular, the forms pertain to E >>
-ε1,
E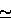 
-ε1 and
E << -ε1
and not to
-ε1 < 1 keV,
-ε1 > 70 keV.
Further, that for
-ε1 > 70 keV
omitted a correction which is increasingly important as E approaches
-ε1. The nature and
magnitude of this latter problem is depicted in
Fig. 1 for uranium. The apparent "edge" is
displaced and offset by several keV with five discontinuities, and at
500 keV (four times the edge energy) the error is of the same magnitude
as Z. This energy range is much higher than that of
Refs. [15,17-21]. In these figures and in the
text, the current formulation avoids or overcomes all problems discussed, as
far as is possible within the prescriptions provided. The use of
f1 as the plotting variable follows the standard of
Refs. [7,16] but more importantly places the
effects on an approximate absolute footing for the real component of the
atomic scattering factor in the forward direction.
