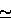 |
 |
 |
|
|
|
-ε1. In any of these
regions where the functional forms are inappropriate, some improvement in
precision can often be gained by using 10-point or higher order Gauss-Legendre
integration. This represents improved precision of the integration using a
less optimum integral transformation.
Previous below-edge errors are illustrated for the K edge of carbon in carbon in Fig. 2. The edge was apparently displaced and asymmetric (typically with a spurious value for the edge itself) as opposed to the revised form ("o" versus "+" in figure). There were also significant errors in the earlier prescription 12% below the edge. This also occurs with similar magnitude (4 e/atom) for the L-edges of uranium at 17-22 keV in Fig 1. These errors occur at energies well within the range of crystallographic investigation and concern, and are not restricted to regimes of specialized anomalous or other diffraction experiments.
The theoretical-experimental synthesis of
Ref. [16] (triangles) is in reasonable
agreement with the current revised results well away from the edge, with the
exception that aliasing is introduced due to the finite logarithmic grid on
which linear interpolation is carried out. This means that the transform is
calculated appropriately from the given absorption coefficients to yield
f1 values for specific energies, but subsequent
interpolation between these points smooths out any finer structure, in
addition to generating an interpolation error even in the absence of
structure. The earlier synthesis [7] contains a
much coarser grid, so direct comparison of the two primarily indicates
interpolation limitations. The relativistic correction factor is only about
0.004 (e/atom or eu in crystallographic notation) and makes negligible
contribution to the results (whatever form is postulated for the correction),
while f0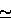
Z-0.04 eu, and does not affect the comparison. Hence a typical
experiment in this regime with graphite or other elemental carbon should
relate to a real component of the atomic scattering factor given to high
precision by f1. The current revised formalism yields a
width (below zero) of 4.6 eV and a mean f1 of circa
-0.9 eu over this region, with f1 = -2.4 eu at
0.24 eV from the edge, or f1 = -4.0 eu at
0.07 eV from the edge (or about the edge width).
The independent particle approximation common to all theories discussed
herein should yield the revised smooth, symmetric form, but the
formalism may be expected to fail near edges or at low energies, where
molecular or collective behavior may occur. However, the revised result is
in good agreement with Cherenkov radiation studies on the carbon K
edge [29], which have derived widths of 5 eV
and a mean susceptibility
χ′ = 0.0016
or f1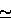
-0.82 eu, and minima of
-2.0 eu > f1,min > -5.1 eu.
Conversely, aliased profiles [16] give minima of
0.3 eu > f1,min > -1.3 eu,
non-aliased transforms of a simple edge structure [30]
yield f1,min from -5.3 eu to
-∞ eu and a width of order
5 eV, while other recent experimental
f″ measurements yielded a width
of around 14 eV and f1,min 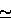-1.2 eu
after integration [31]. All are in disagreement
with the Cherenkov studies. In this respect, the importance of direct
measurements of the scattering factor (anomalous or atomic) cannot be
overestimated. Finally, the result of Ref. [21],
which might be expected to include contributing collective behavior, appears
to give a shift and singularity in the structure [15].
|
||||
